Experimental Comparisons of Convergence Robustness Between First Order Adaptive Learning Rate Optimizers
Abstract
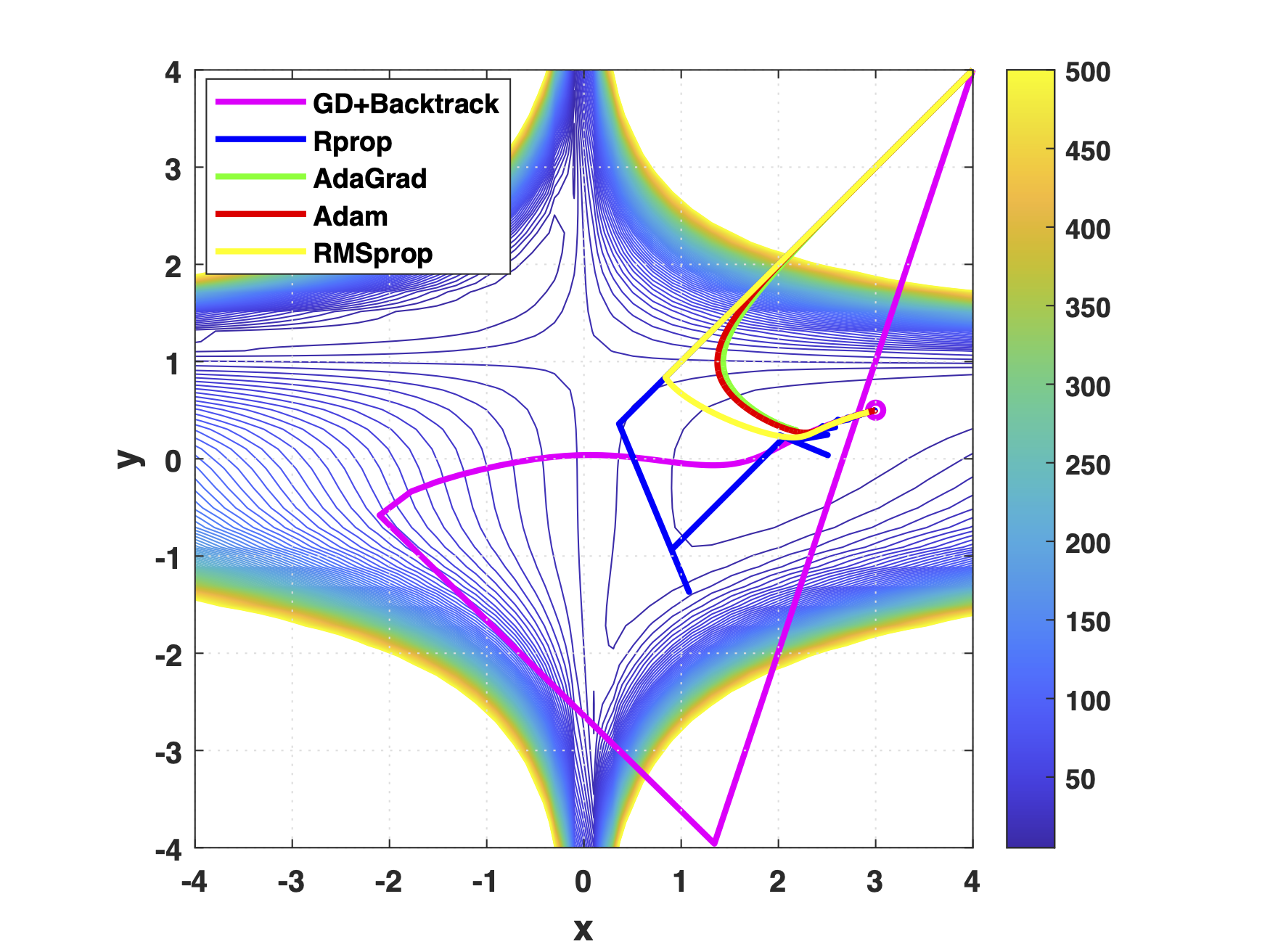
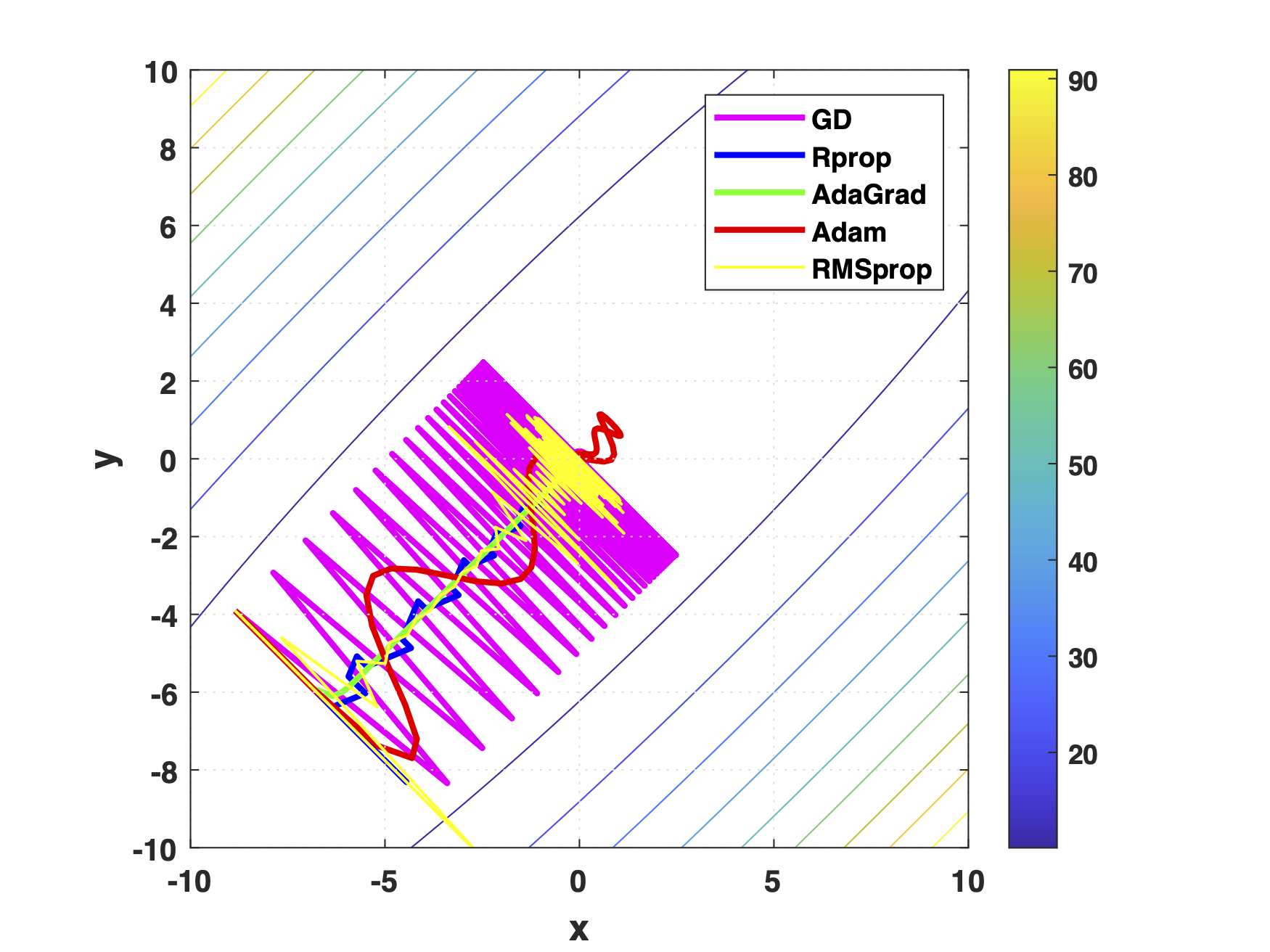
Learning rate is an essential hyper-parameter to be tuned for gradient descent optimizers. While methods such as scheduled learning rate decay and backtracking line search of step size are often suggested for gradient descent algorithms to have theoretically-proved convergence rates, in general realistic optimization tasks such as training neural networks, optimizers with adaptive learning rate are often preferred due to their robustness and good empirical performances under a wide range of learning rate settings. This experimental study compares the performance of 4 commonly-used adaptive learning rate optimizers, including Rprop, RMSprop, AdaGrad and Adam, against vanilla gradient descent algorithm using fixed, decayed, and backtracked learning rate. The optimizers were tested with a wide range of learning rate settings on sphere, Matyas, Beale and Ackley functions to examine their convergence on unconstrained optimization tasks with different convexity and gradient property. Results showed that the adaptive learning rate algorithms generally have wide range of acceptable learning rates, being easier to use than the the gradient descent optimizers, but could fail to converge in situations where gradient descent with backtracking line search can converge.